The Pythagorean formula for tangents and secants There's also one for cotangents and cosecants, but as cotangents and cosecants are rarely needed, it's unnecessary Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulasHence, the TAN function can be used in two ways, ie worksheet function in which the formula of TAN function needs toThe period of the tan(2x) tan (2 x) function is π 2 π 2 so values will repeat every π 2 π 2 radians in both directions x = π 8 πn 2, 5π 8 πn 2 x = π 8 π n 2, 5 π 8 π n 2, for any integer n n
Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities
Tan 2x formula in terms of cos x
Tan 2x formula in terms of cos x-Solve for x tan(2x)tan(x)=1 Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Replace with in the formula for period Solve the equation Tap for more steps The absolute value is the distance between a number and zero The Parameters or Arguments Number it is the number or numeric value for which tangent needs to be calculated of an angle Result TAN function always returns the numeric value after applying to a particular cell Type Worksheet function;



Ilectureonline
Tan 2x = Double angle function of tan x and tan 2 x = Square funtion of tan x What Is tan2x Formula in Terms of Sin x?Tan 2x formula in trigonometry is given as, tan 2x = 2tan x / 1−tan 2 x, where, tan x = Opposite Side / Adjacent Side;About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
Tan 2x ≠ 2 tan x by Shavana Gonzalez Variation of lab bhattacharjee's answer $$\tan^2x=\tan(xa)·\tan(xb) \Rightarrow \\ \tan^2x1=\tan(xa)·\tan(xb)1 \Rightarrow \\ \frac{1}{\cos^2 x}=\tan(xa)·\tan(xb)1 \Rightarrow \\ \cos^2x =\frac1{\tan(xa)·\tan(xb)1} \Rightarrow \\ \frac{1\cos 2x}{2}=\frac1{\tan(xa)·\tan(xb)1} \Rightarrow \\\\ \cos 2x=\frac2{\tan(xa)·\tan(xb)1}1 \Rightarrow \\ \cos 2x=\frac{1\tan (xa)\cdot \tan (xb)}{1\tan (xa)\cdot \tan\(\cos 2X = \frac{\cos ^{2}X – \sin ^{2}X}{\cos ^{2}X \sin ^{2}X} Since, cos ^{2}X \sin ^{2}X = 1 \) Dividing both numerator and denominator by \(\cos ^{2}\)X, we get \(\cos 2X = \frac{1\tan ^{2}X}{1\tan ^{2}X} Since, \tan X = \frac{\sin X}{\cos X} \)
You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3 There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² ATrigonometric function of cos 2A in terms of tan A is also known as one of the double angle formula We know if A is a number or angle then we have, cos 2A = cos2 A sin2 A cos 2A = c o s 2 A − s i n 2 A c o s 2 A ∙ cos2 A ⇒ cos 2A = cos2 A (1 tan2 A)
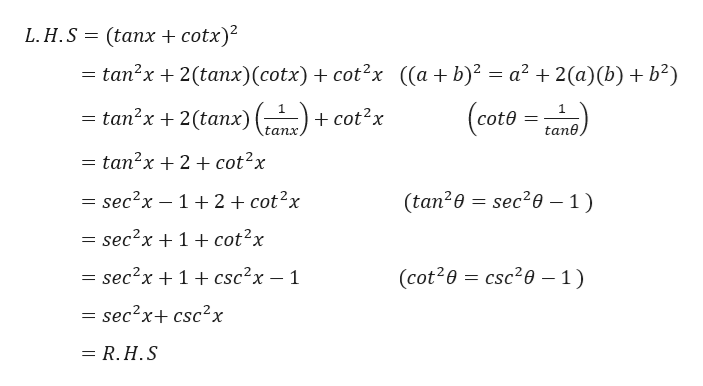



Answered The Question Says To Confirm That The Bartleby




Multiple Angle Formulas Overview Video Trigonometry Ck 12 Foundation
Our given expression is tan(2x y) tan(2x – y) = 1 Formula used When A B = 90° then, tanA tanB = 1 and vice versa Calculation Our given expression is tan(2x y) tan(2x – y) = 1 ⇒ 2x y 2x – y = 90° ⇒ 4x = 90° ⇒ 2x = 45° Now, tan2x = tan45° = 1 ∴ The value of tan45° is 1 Download Question With Solution PDF ››= 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;Verify cos x (cos x/ (1 – tan x)) = (sin x cox x)/ (sin x – cos x) 355 Integral of (e^2x 1)/ (e^2x 1) 405 tan (A B) tan (x y) tan (A B) tan (x y) 250 Switch camera



Knoxschools Instructure Com Files 7731 Download Download Frd 1 Verifier Nwvnfhcqjj3uwbxvthab5cvl9gai66hcxz8iywsc




Tinkutara Equation Editor Math Forum Question
Tan2x Formulas Tan2x Formula = \\frac{2\text{tan x}}{1 tan^{2}x}\ We know that tan(x) = sin(x)/cos(x) Then, tan2x formula = sin(2x)/cos(2x) Tan 2x can also be written in terms of sin x and cos x, Tan2x Formula in terms of cos x = \\frac{2 sin(x) cos(x)}{cos^{2}x cos(ax)cos(bx) = 1 2cos((a − b)x) 1 2cos((a b)x) These formulas may be derived from the sumofangle formulas for sine and cosine Example 726 Evaluating ∫ sin(ax)cos(bx)dx Evaluate ∫sin(5x)cos(3x)dx Solution Apply the identity sin(5x)cos(3x) = 1 2sin(2x) 1 2sin(8x)The tan squared function rule is also popularly expressed in two forms in trigonometry $\tan^2{x} \,=\, \sec^2{x}1$ $\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof



1
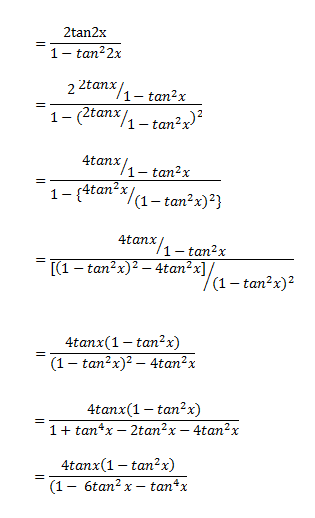



Trigonometry Functions Class Xi Exercise 3 3 Breath Math
Formulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angle double of the angle present in their formulas Sin 2x Formula Sin 2x formula is 2sinxcosx Image will be uploaded soon Sin 2x =2 sinx cosx Derivation of Sin2x Formula f (g (x)) = tan (2x) ⇒ f' (g (x)) = sec2(2x) = 2sec 2 (2x) Using the chain rule, the derivative of tan (2x) is 2sec2(2x) Finally, just a note on syntax and notation tan (2x) is sometimes written in the forms below (with the derivative as per the calculation above) Just be aware that not all of the forms below are mathematically correct tan2xTan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle sin 1 y q==y 1 csc y q= cos 1 x q==x 1 sec x q= tan y x q= cot x y q= Formulas and Identities Tangent and Cotangent Identities sincos tancot cossin qq qq qq == Reciprocal Identities 11 cscsin sincsc 11 seccos cossec 11 cottan tancot qq qq qq



Mafiadoc Com Download Section 73 Double Angle Half Angle And Sum Product Identities 59d8ddd0fc79f562c Html




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
2 tanx 1 − tan2x = 2 sinx cosx 1 − (sin2x cos2x) = 2sinx cosx cos2x −sin2x = sin2x cos2x = tan2x Proofs for sin2x = 2sinxcosx and cos2x = 1 −2sin2xFormula for Lowering Power tan^2 (x)=?Double angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 x



What Is The Formula Of Tan2x Quora



1
Cos 2x ≠ 2 cos x; Get an answer for 'Prove the following reduction formula integrate of (tan^(n)x) dx= (tan^(n1)x)/(n1) integrate of (tan^(n2))dx' and find homework help for other Math questions atTan (x) is an odd function which is symmetric about its origin tan (2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin (2x) to cos (2x) sin (2x) = 2 sin (x) cos (x) cos (2x) = (cos (x))^2 – (sin (x))^2 = 1 – 2 (sin (x))^2 = 2




What Is Integral Of Sin2x Tan2x Quora




Tangent Half Angle Formula Wikipedia
Homework Statement cosx=12/13 3pi/2 is less than or equal to x is less than or equal to 2pi Homework Equations sin2x = 2sinxcosx cos2x = 12(sinx)^2 tan2x = (2tanx)/(1(tanx)^2) The Attempt at a Solution Using the tan2x formula, I get 60/47 UsingYou need to write sin 2x and cos 2x in terms of tanx such that `sin 2x = (2 tan x)/(1 tan^2 x); Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes
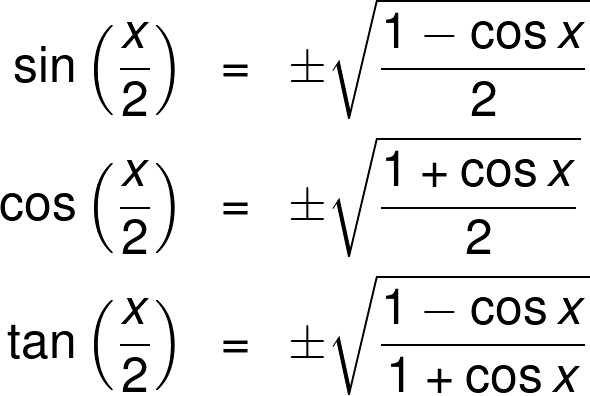



Half Angle Calculator




Differentiate The Following From First Principle Tan 2x
Solution for a Let cosx = () and cos x lies below the x axis Find sin(2x), cos(2x) and tan(2x) b Proof the formula of unit circle x?The functions sine, cosine and tangent of an angle are sometimes referred to as the primary or basic trigonometric functions Their usual abbreviations are (), (), and (), respectively, where denotes the angle The parentheses around the argument of the functions are often omitted, eg, and , if an interpretation is unambiguously possible The sine of an angle is defined Transcript Example 27 find the value of tan 𝜋/8 tan 𝜋/8 Putting π = 180° = tan (180°)/8 = tan (45°)/2 We find tan (45°)/2 using tan 2x formula tan 2x




Integrate Tan 2x




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
I know that and The next step would then be to say that but now what?Formula cos 2 θ = 1 − tan 2 θ 1 tan 2 θ A mathematical identity that expresses the expansion of cosine of double angle in terms of tan squared of angle is called the cosine of double angle identity in tangentCos 2x = (1tan^2 x)/(1 tan^2 x)` Plugging `tan x = sqrt6/3` in the formulas above yields



Www Mayfieldschools Org Downloads 4 8 double angle formulas answers Pdf




Ex 3 3 Q23 Prove That Tan4x 4tanx 1 Tan 2x 1 6tan 2x Tan 4x
General solution of tan(2x)tan(x) = 1 For the question, tan(2x)tanx = 1, I divided it by tanx, and got the solution as ( 2n 1) π 6 tan2x = cotx = tan(π 2 − x) So, 2x = nπ π 2 − x So, 3x = ( 2n 1) π 2 But the book solved using the formula of tan(2x), and got the solution as ( 6n ± 1) π 6 I can see that my solution has odd Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and Using cos (x y) = cos x cos y – sin x sin y = cos x cos x – sin x sin x = cos 2 x – sin 2 x Putting cos 2 x = 1 – sin 2 x cos 2x = cos 2 x – sin 2 x = 1 – sin 2 x – sin 2 x = 1 – 2sin 2 x Putting sin 2 x = 1 – cos 2 x cos 2x = cos 2 x – sin 2 x




How To Graph Tan Ex Y Tan2x Study Com




Double Angles Ppt Video Online Download
Therefore, tan 60° = \(\frac{2 tan 30°}{1 tan^{2} 30°}\) (ii) The above formula is also known as double angle formulae for tan 2A Now, we will apply the formula of multiple angle of tan 2A in terms of A or tan 2A in terms of tan A to solve the below problem 1 Express tan 4A in terms of tan A Solution tan 4a = tan (2 ∙ 2A)Sin 2x formula is known as the double angle formula In this formula, we find the sine of the angle whose value is doubled We are familiar that sin is one of the primary trigonometric ratios that can be defined as the ratio of the length of the perpendicular to that of the length of the hypotenuse in a rightangled triangleYou could take tan(x) out of the fraction, but I still don't know how to go about simplifying it The book says the answer is




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




14 2 Trigonometric Identities
Tan α = 2 tan α 2 1 − tan 2 α 2 {\displaystyle \tan \alpha = {\frac {2\tan {\frac {\alpha } {2}}} {1\tan ^ {2} {\frac {\alpha } {2}}}}} Combining the Pythagorean identity with the doubleangle formula for the cosine, cos 2 α = cos 2 α − sin 2 α = 1 − 2 sin 2 α = 2 cos 2 α − 1 {\displaystyle \cos 2\alpha =\cos ^ {2}\alpha \sin ^ {2}\alpha =12\sin ^ {2}\alpha =2\cos ^ {2}\alpha 1} Find the exact value of `cos 2x` if `sin x= 12/13` (in Quadrant III) Answer Using the following form of the cosine of a double angle formula, cos 2 α = 1− 2sin 2 α , we have Formulas expressing trigonometric functions of an angle 2x in terms of functions of an angle x, sin(2x) = 2sinxcosx (1) cos(2x) = cos^2xsin^2x (2) = 2cos^2x1 (3) = 12sin^2x (4) tan(2x) = (2tanx)/(1tan^2x)




Verify A Trigonometric Identity Ppt Video Online Download




Solve The Equation Tan 2x Cot X Pi 6
Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1Proof sin^2 (x)= (1cos2x)/2 Proof cos^2 (x)= (1cos2x)/2 Proof Half Angle Formula sin (x/2)The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle




Small Angle Approximation Brilliant Math Science Wiki




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
Explain how to determine the doubleangle formula for tan(2x) tan ( 2 x) using the doubleangle formulas for cos(2x) cos ( 2 x) and sin(2x) sin ( 2 x) 3 We can determine the halfangle formula for tan(x 2) = √1−cosx √1cosx tan




Tangent Half Angle Formula Wikipedia



Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities




Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath



Ilectureonline




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com
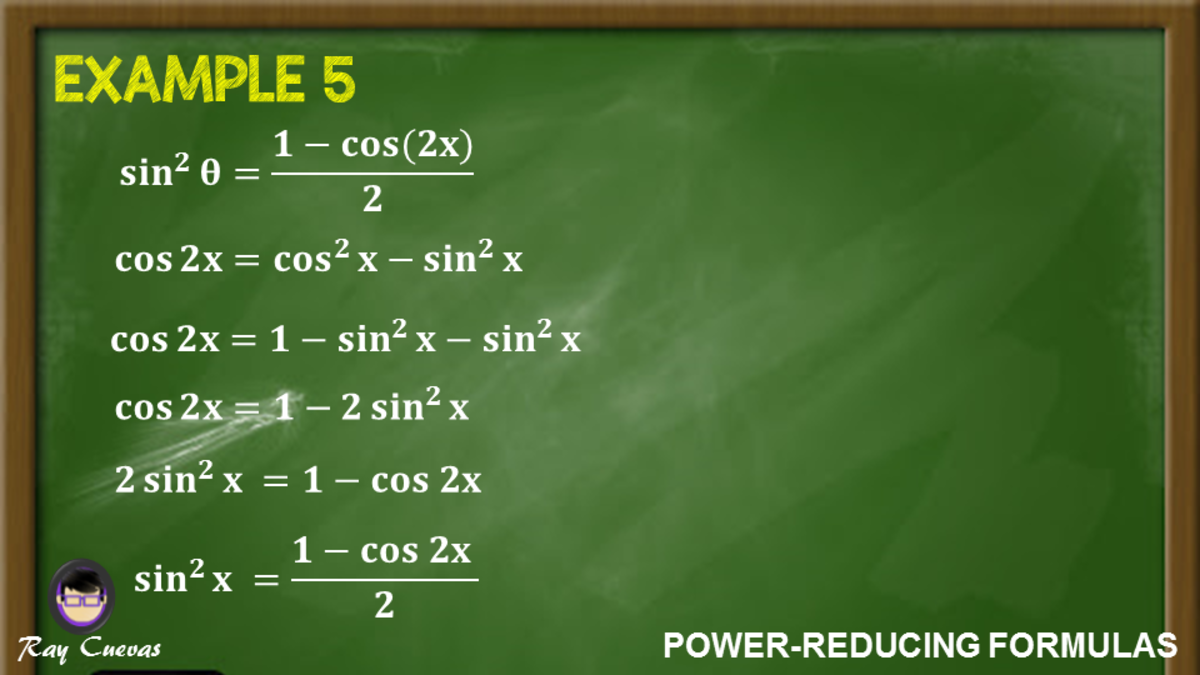



Power Reducing Formulas And How To Use Them With Examples Owlcation



Establish The Given Limit Formula Stumbling Robot




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Ilectureonline




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction



Elementary Calculus Theorem 1




Integration 05 Today S Objectives Integrating Products
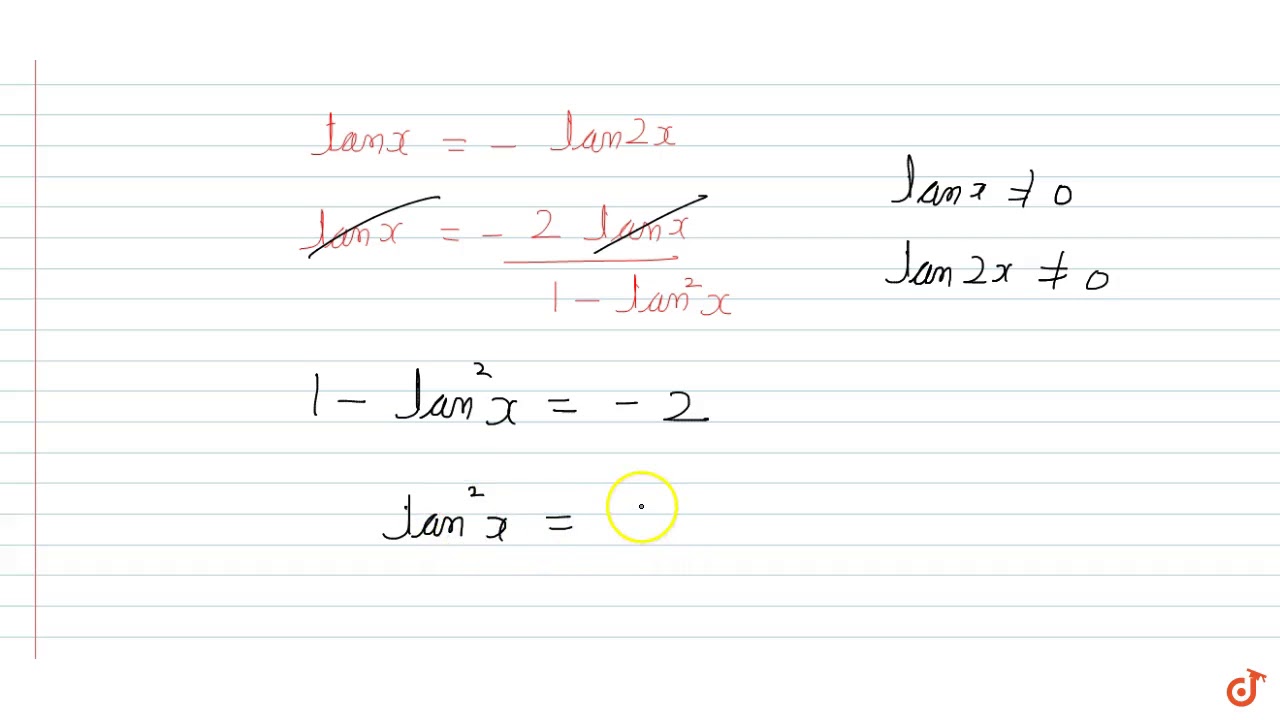



The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is Youtube
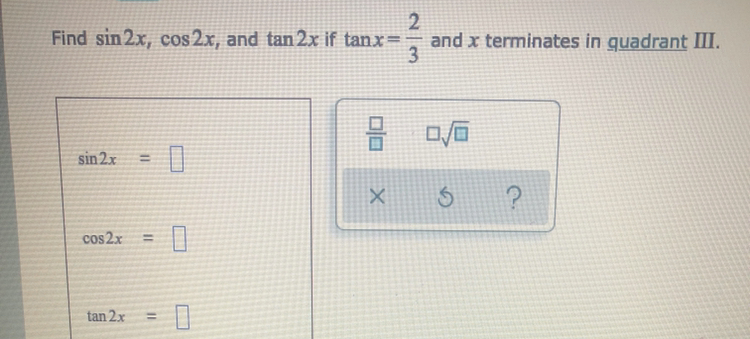



Answered Find Sin 2x Cos 2x And Tan 2x If Bartleby




Cos 2x Formula Trigonometry Formula




Prove The Identity 3 Tan 3x 9 Tan X 3 Tanx 13 Chegg Com



Differentiate The Following From First Principles I Tan 2 X Ii Tan 2x 1 Sarthaks Econnect Largest Online Education Community
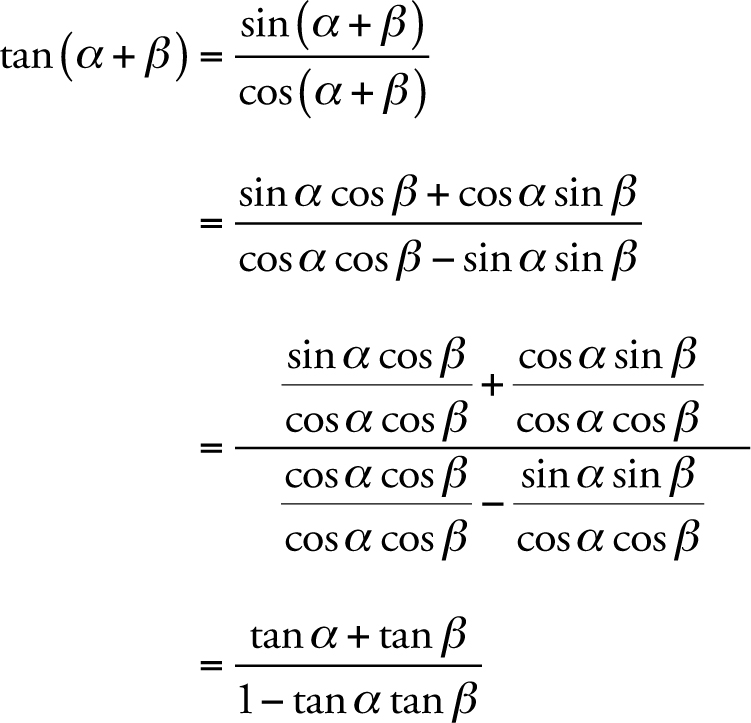



Tangent Identities



Tangent Identities
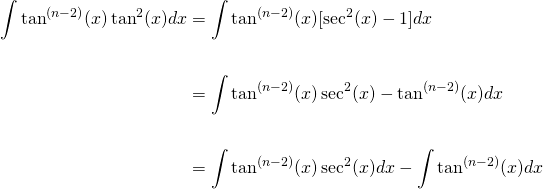



Reduction Formula For The Integral Of Tan N X Dx Steemit




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube
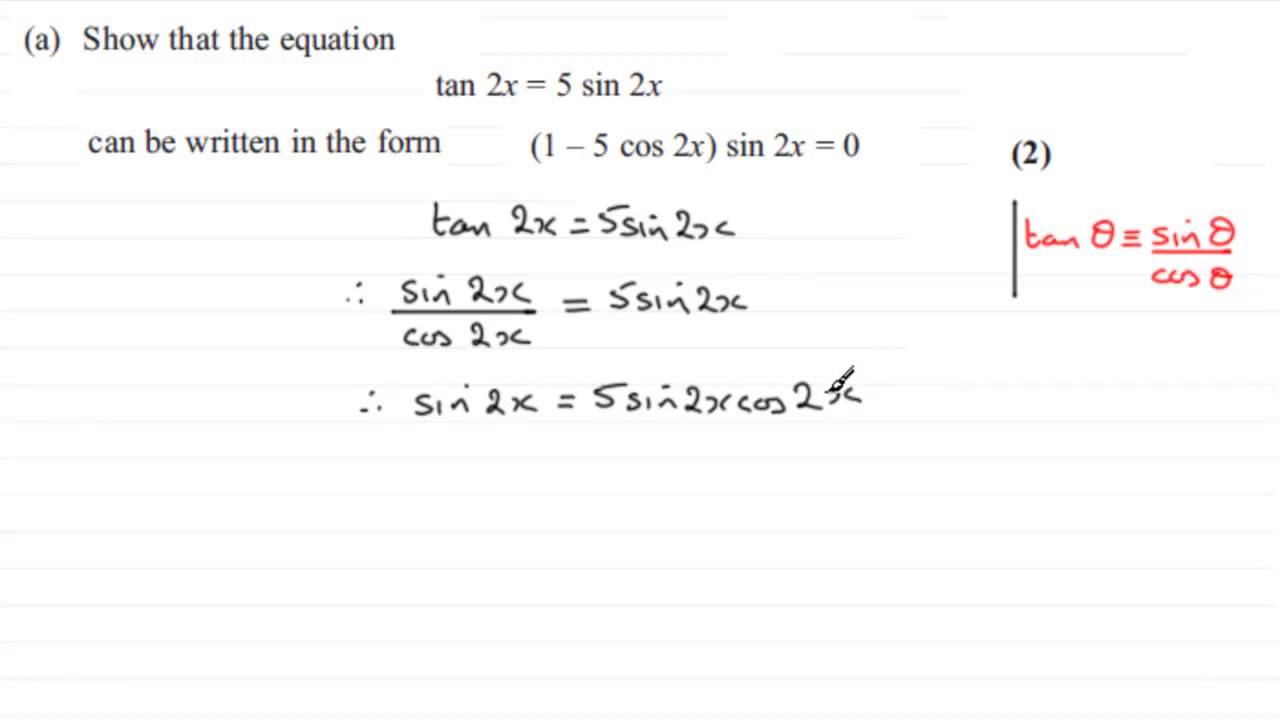



Edexcel Core Mathematics C2 June 12 Solutions Examples Worksheets Videos Activities




Trigonometric Identities Edexcel A Level Maths Pure Revision Notes



Solution Determine The Period Of Y Tan 2x




Sin2x Cos2x 1 Proof




Integrate Sec 2x Method 2




Trig Identity Sec2x Minus Tan2x T10 Youtube



Cos2x Identity




Integrate Tan 2x By Parts
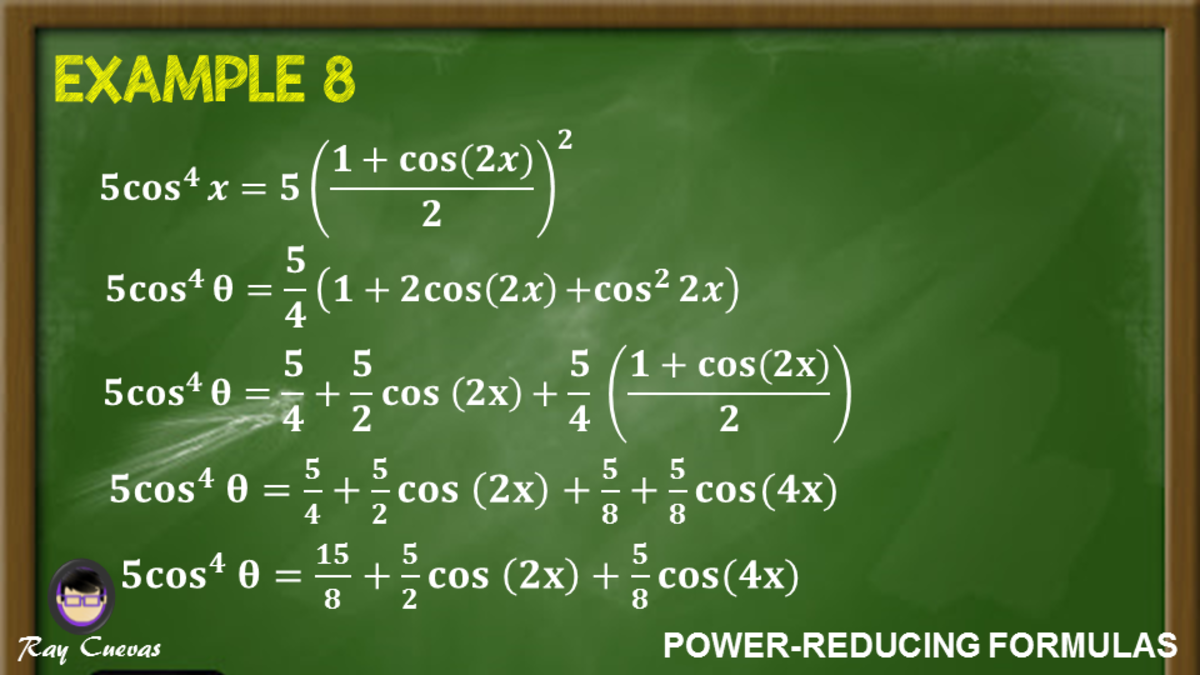



Power Reducing Formulas And How To Use Them With Examples Owlcation




Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Ppt Download




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Trig Identities Hsn Forum




Ch 5 5 Multiple Angle And Product To Sum Formulas Ppt Download Free Math Help Math Review Worksheets Trigonometry



Prove Sin2x 2tanx 1 Tan 2x Socratic



1




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help




Art Of Problem Solving



Www Drfrostmaths Com Getfile Php Fid 479
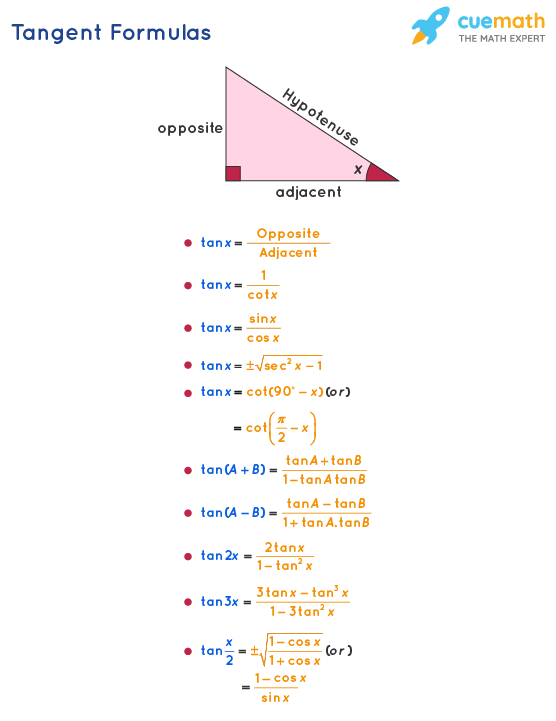



Tangent Formula What Are Tangent Formulas Examples



Differentiate The Following W R T X Tan 1 3 2x 1 6x Maths Pyranic




Math34 Trigonometric Formulas




Tan 2x Formula What Is Tan 2x Formula Examples




How To Find The Inverse Of A Trig Function Dummies



Yorkshiremathstutor Com Wp Content Uploads 19 02 8 Differentiation Answers Pdf



Solution Verify The Identity By Showing That The Left Equals Right Sec 2x 1 Tan 2 Sec2x Do I Use 1 Cos 2x 1 Tan 2x Or Do I Use 1 Tan 2x 1 Tan 2x Either Way I Do Not Know Where To Go Fro



Points Or No Points Maths Sl Ib Survival



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf



Trig Identity Question




Double Angle Identities Solutions Examples Videos Worksheets Games Activities
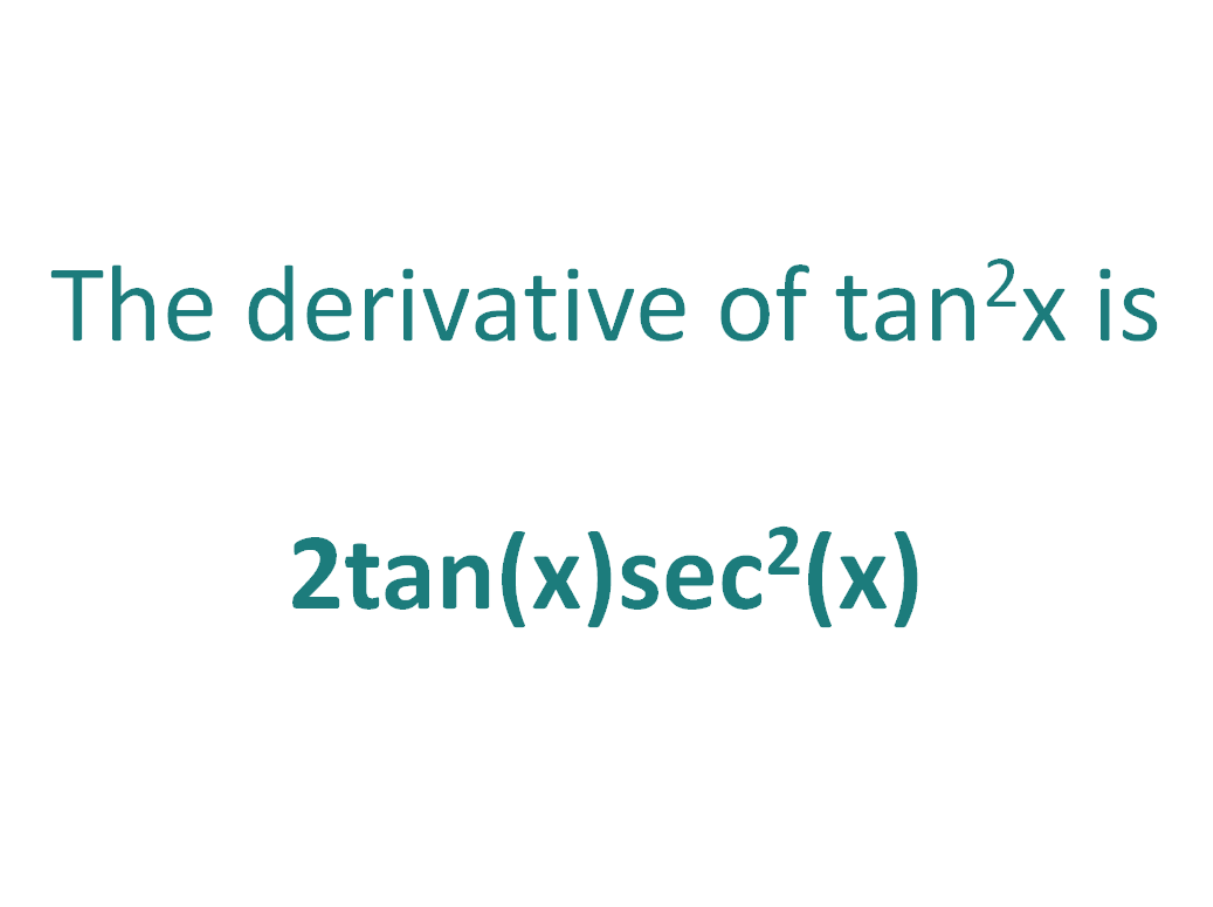



The Derivative Of Tan 2x Derivativeit




Math34 Trigonometric Formulas




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In




Prove The Identity 2 Tan 3x Stan X 2tan3 X 1 3 Tan Chegg Com




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Weierstrass Substitution Wikipedia
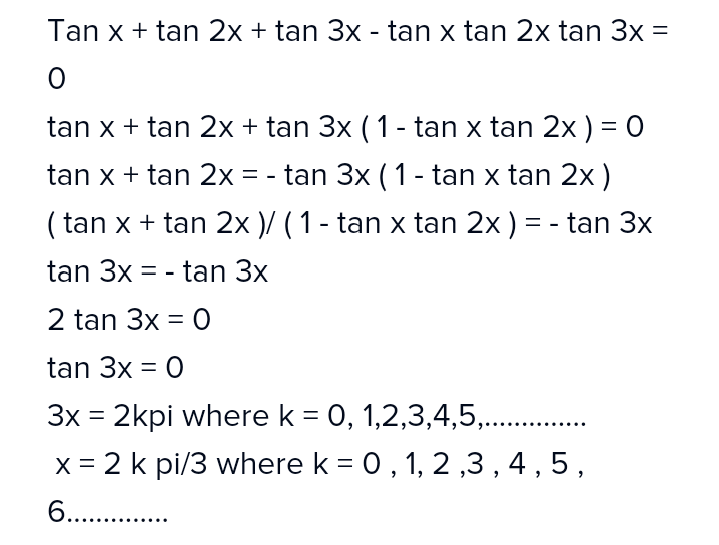



Solve Tanx Tan2x Tan3x Tanxtan2xtan3x




Section 7 3 Double Angle Half Angle And Sum




Double Angle Properties Rules Formula Examples Video Lesson Transcript Study Com



Tan2x ただの悪魔の画像



Solved Givencos 3 0 5 Findtan2 6 Use The Formulatan2x 1 Cos2x 1 Cos2x Course Hero




14 2 Trigonometric Identities




Find Sin 2x Cos 2x And Tan 2x If If Tan X 2 And Gauthmath




Lesson 4 5 Double Angle Formulas



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau



Prove The Identity Tan P 4 X Tan P 4 X 2 Sec 2x Sarthaks Econnect Largest Online Education Community




The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2 0 Is




What Is The Integration Of Tan 2x Solution Quora



bestpictjcry Tan 2x Tan 2x








Example 5 Verify A Trigonometric Identity Verify The
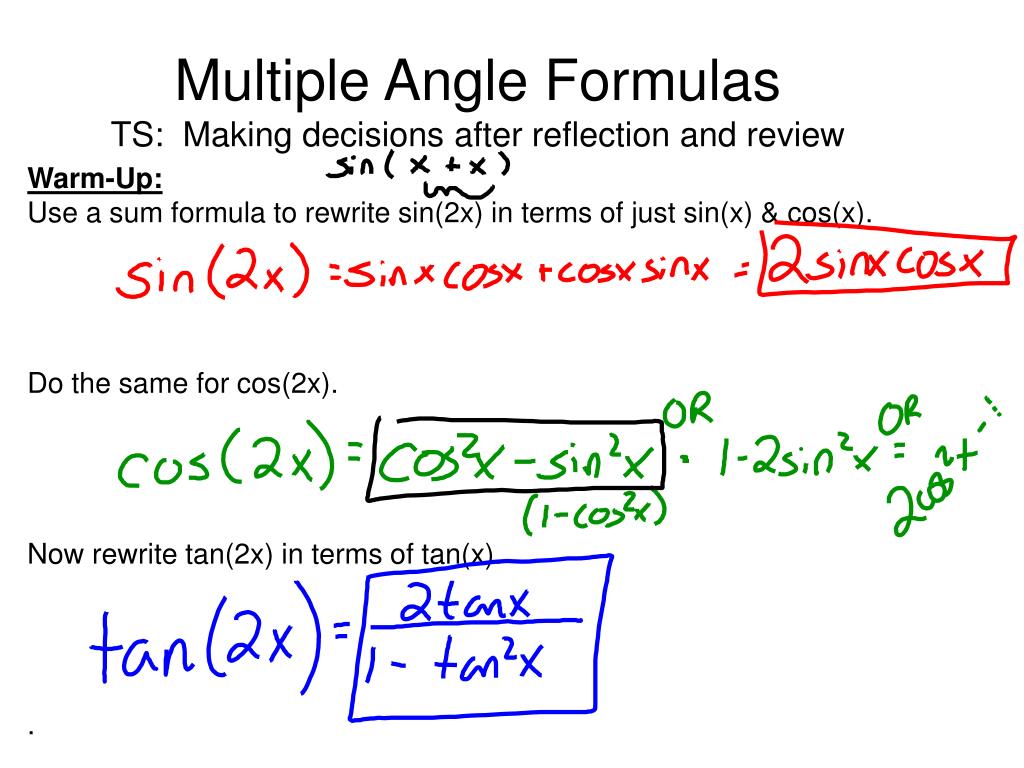



Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id
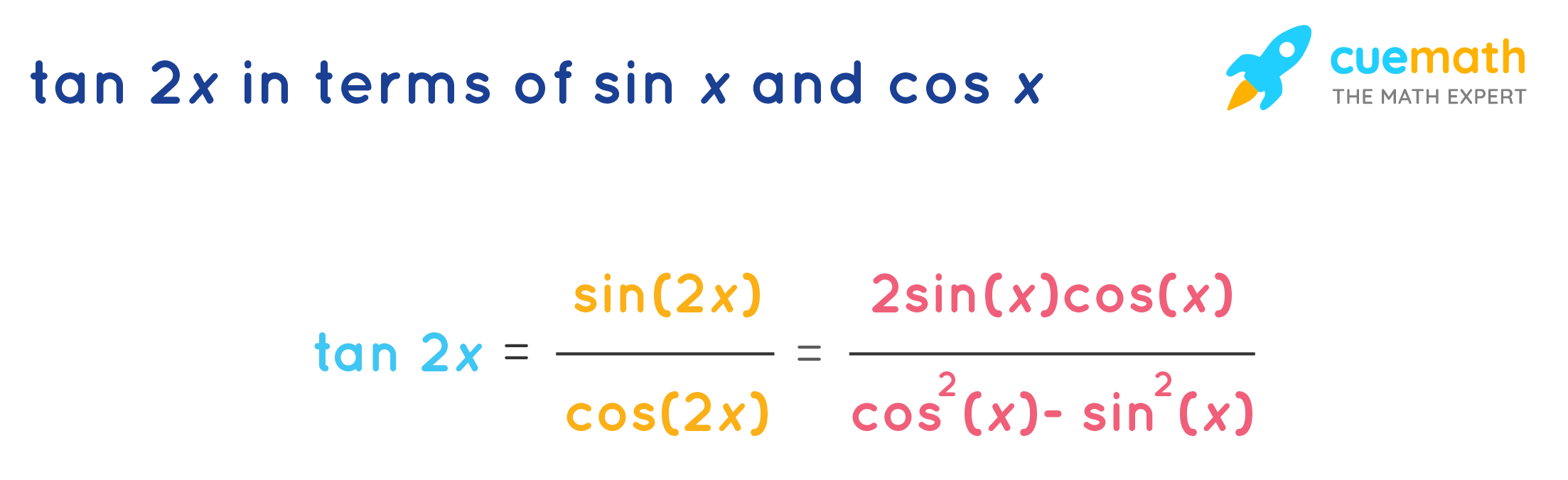



Tan 2x Formula What Is Tan 2x Formula Examples
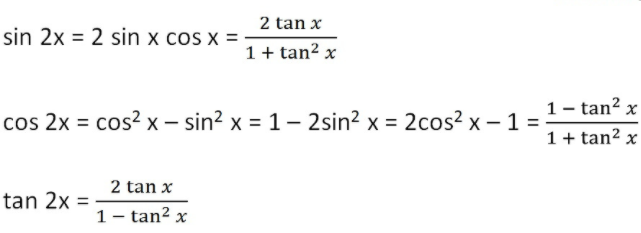



Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec




Ashley Avery Free Books Catalog



Biomath Trigonometric Functions



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com



No comments:
Post a Comment